Mathematics of Golf

free golf tips, golf instruction, lessons, lower score, equipment used for golf, golf swing, golf ball , golf ball review

Probable GOLF Instruction
Expertly Shaping Swings & Trajectories
Solving your errant golf ball problems

New -- Social Golfer Combinations

Having Children

What is the likelihood of having 3 boys and 1 girl? Below is a list
of the possible outcomes.

BBBB GBBB GGBB GGGB GGGG

BGBB GBGB GGBG

BBGB GBBG GBGG

BBBG BGGB BGGG

BBGG

BGBG

There are 16 possible outcomes when having four children. Note
that there are 4 possible ways of having 3 boys and 1 girl
(GBBB, BGBB, BBGB, BBBG). Thus the probability of having
3 boys and 1 girl is 4/16 or 0.25 (25%). If one were to take
a random sample of 50 families with 4 children each, one would
expect to find that 12.5 families (0.25 x 50), on average, would
have 3 boys and 1 girl. The proba- bility of having 4 boys would
be 1/16 or 0.0625 (6.25%) and in a sample of 50 families, one
would expect to find that 3.1 families, on average, would have
4 boys.

Golf Shot Patterns

So, to calculate, on average, the expected number of times out
of 50 shots you would hit the ball 10 yards left and 10 yards
short of your target, you would use E = P x 50, where P is the
probability of hitting the ball to that position. You would calcu-
late P by dividing the number of times you hit to that position by
the total number of shots. The greater the number of shots,
the more accurate your estimate of probability.

By documenting how many times you hit the ball to all the
possible positions relative to your target, you can calculate the
respective probabilities. Below is a summary of my shot pattern
with medium irons 5 thru 7.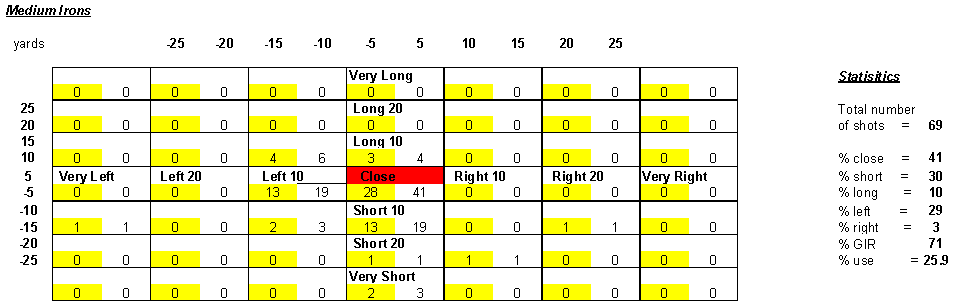

Each of the yellow cells contains the number of times I hit to
that position, relative to my target. Out of 69 shots, I hit within
5 yards of my target 13 times. If I were to continue that shot
pattern, the probability of hitting within 5 yards of my target in
the future would be 13/69 or about 18.8%. Likewise, I hit
10 yards short and 10 yards left 2 out of 69 shots, or 2.9%
of the time.

To calculate the expected score on a hole, one needs to
combine the shot pattern above with the target and its sur-
roundings. For instance, if I were to aim at the pin when it is
cut 10 yards short and 10 yards left of the center of the
green described earlier, then:

I would have an 18.8% chance of hitting with 5 yards of
the pin. From there, I would likely take 1.6 putts to hole out
based on my putting statistics (shown below). Thus there is
an 18.8% chance of scoring 2.6 on the hole.

I would have a 2.9% chance of hitting 10 yards short and
10 yards left. With this pin placement, the shot would land in
the water hazard. I would drop in front of the hazard, play
about a 60 yard pitch, hopefully hit the green, and then putt
out. My expected score would depend on my pitching ability
(past statistics indicating how close I would likely pitch the
ball) and then on my putting ability (see below). My expected
number of shots from 50 yards is 2.77. Thus I would have
a 2.9% chance of scoring a 4.77 on the hole, likely a double-
bogey.

If one adds the probabilities of each region in my shot pattern
together, they will add to 100%. This means that there is a
100% chance of hitting the next shot somewhere within the
shot pattern (excluding a few of those really ugly shots which
don't truly represent my ability). To calculate the expected
score on a given shot, one must add the expected outcomes
from each region.

E = P x score + P x score + P x score + . . . . . . + P x score

= 0.188 x 2.6 + 0.029 x 4.77 + . . . . . .

= with 5 yds + 10 yd left, 10 yd short + . . . . . .

= 4.32

Adding together each expected score from each region
multiplied by the probability of hitting each region yields 4.32
strokes. Thus, if I were to aim at the pin when it is 10 yards
left and 10 yards short of the middle of the green, I would
most likely score 4.32, on average. Sometimes I would make 2,
sometimes 3, sometimes 4 or 5 or even 6. The average would
be 4.32. I would likely lose the hole if in a match.

Mathematics of Predicting Outcomes of Shots

Rolling Dice

Consider rolling a pair of dice. What is the probability of
rolling a 7? One can answer this question by analyzing the total
possible number of different outcomes of rolling the dice.
With a pair of dice, one can roll the numbers 2 thru 12. There
is only one way to roll a 2 (1 & 1), two ways of rolling a 3
(1 & 2 or 2 & 1), 3 ways of rolling a 4 (1 & 3, 3 & 1, 2 & 2), etc.
The number of ways to roll each outcome is summarized in the
table below. The 1st row lists the possible outcomes, the 2nd
row lists the number of each possible outcome, and the 3rd
row lists the probability of each possible outcome.

1	2	3	4	5	6	7	8	9	10	11	12
0	1	2	3	4	5	6	5	4	3	2	1
0	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

Note that there are 6 possible ways of rolling a 7 (4 & 3, 3 & 4,
5 & 2, 2 & 5, 6 & 1, 1 & 6) and that there are 36 total possible
outcomes. Therefore, the probability of rolling a 7 is 7/36 or
about 0.194, which means there is a 19.4% chance of rolling a 7,
assuming the dice are not biased in any way. The probability of
rolling a 2is 1/36 or about 0.0278 (2.78%).

The laws of probability state that to determine how many
times an expected outcome, E, (due to chance) will occur, one
needs to know the probability, P, of the outcome and the number
of trials, N, to achieve the outcome. The equation is:

E = P x N

Perform the following experiment. Roll a pair of dice 50 times
and count the number of times you roll a 7 and a 2. If you
were to repeat this experiment many times, you would likely roll
a 7 a total of 9.7 times ( 0.194 x 50) and a 2 a total of 1.4
times (0.0278 x 50). Of course the 9.7 and 1.4 are averages of
what you would observe. In one experiment you might roll a 7
a total of 12 times and in the next experiment it might be
8 times.

Langley, B.C. V2Y 2G4 Canada
Phone: 604-309-7030 FAX: to fax, email an attachment
probablegolf@yahoo.ca or golfexpert@probablegolfinstruction.com

Site maintained by Ken Tannar.

This page in other languages: chinese, deutsch, espanol, francais, japanese, korean

GOLF ASSISTANTS